Линейные
уравнения первого порядка и уравнения, сводящиеся к ним.
Дифференциальное
уравнение вида
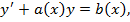
где функции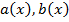 
непрерывны на некотором интервале 
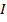, называется линейным
дифференциальным уравнением первого порядка.
Решается это
уравнение следующим образом. Сначала решаем однородное уравнение (ОУ): (2)
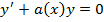
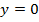– решение этого уравнения. Пусть 
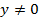. Так как 
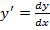, то
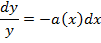
Решение
этого уравнения
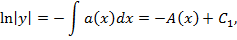
где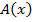 
– некоторая первообразная функции 
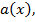a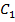 
– произвольная постоянная. С учётом решения 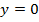общее решение однородного уравнения
записывается в виде (3)
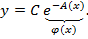
Далее
применяем метод вариации постоянной (ВП): в уравнении (1) сделаем замену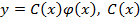 
– новая неизвестная функция. Подставим 
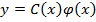в уравнение (1):
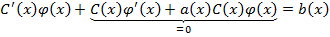
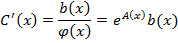
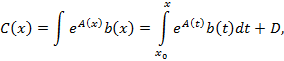
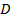– произвольная постоянная. Отсюда получаем общее решение
уравнения (1):
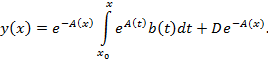
Пример. Решить уравнение
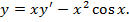
Решение. Решаем однородное уравнение
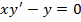
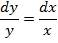
отсюда
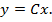
Метод
вариации постоянной (ВП): в исходном уравнении делаем замену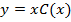 
:
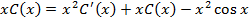
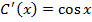
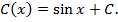
Тогда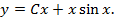 
Уравнение
Бернулли.
Уравнением
Бернулли называется уравнение вида
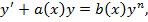
где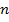 
– натуральное число,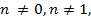 
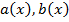– непрерывные на интервале 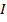функции.
Если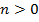 
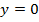, то – решение. Пусть 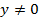. Поделим уравнение на 
:
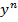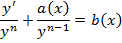
и сделаем
замену
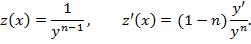
Получили
уравнение
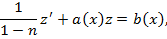
которое
является линейным относительно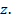 
Пример. Решить уравнение
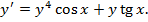
Решение.
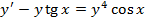
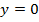– решение. Пусть 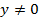. Поделим уравнение на 
:
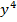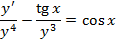
Сделаем
замену
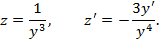
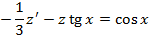
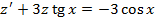
Решаем ОУ:
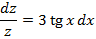
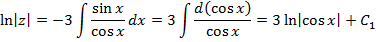
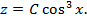
Метод ВП:
В исходном
уравнении делаем замену
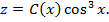
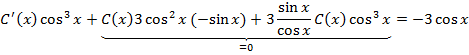
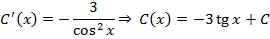
Тогда
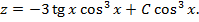
Ответ: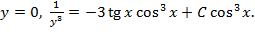 
Уравнение
Риккати.
Уравнением
Риккати называется уравнение вида
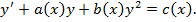
В общем
случае уравнение Риккати не выражается через элементарные функции с помощью
конечного числа арифметических операций, суперпозиций и операций взятия
первообразных (говорят, что уравнение не разрешимо в квадратурах). Но если
известно частное решение уравнения Риккати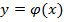 
, то заменой 
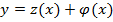уравнение Риккати сводится к
уравнению Бернулли.
